11.2.1三角形全等的判定(SSS)
一、教学内容
本节课主要内容是探索三角形全等的条件(SSS),及利用全等三角形进行证明.
二、教学目标
(一)知识与技能
了解三角形的稳定性,会应用“边边边”判定两个三角形全等.
(二)过程与方法
经历探索“边边边”判定全等三角形的过程,解决简单的问题.
(三)情感、态度与价值观
培养有条理的思考和表达能力,形成良好的合作意识.
三、重、难点与关键
(一)重点:掌握“边边边”判定两个三角形全等的方法.
(二)难点:理解证明的基本过程,学会综合分析法.
(三)关键:掌握图形特征,寻找适合条件的两个三角形.
四、教具准备
一块形状如图1所示的硬纸片,直尺,圆规.

五、教学方法
采用“操作──实验”的教学方法,让学生亲自动手,形成直观形象.
六、教学过程
(一)设疑求解,操作感知
【教师活动】(出示教具)
问题提出:一块三角形的玻璃损坏后,只剩下如图2所示的残片,你对图中的残片作哪些测量,就可以割取符合规格的三角形玻璃,与同伴交流.
【学生活动】观察,思考,回答教师的问题.方法如下:可以将图1的玻璃碎片放在一块纸板上,然后用直尺和铅笔或水笔画出一块完整的三角形.如图2,剪下模板就可去割玻璃了.
【理论认知】
如果△ABC≌△A′B′C′,那么它们的对应边相等,对应角相等.反之,如果△ABC与△A′B′C′满足三条边对应相等,三个角对应相等,即AB=A′B′,BC=B′C′,CA=C′A′,∠A=∠A′,∠B=∠B′,∠C=∠C′.
这六个条件,就能保证△ABC≌△A′B′C′,从刚才的实践我们可以发现:只要两个三角形三条对应边相等,就可以保证这两块三角形全等.
信不信?
【作图验证】(用直尺和圆规)
先任意画出一个△ABC,再画一个△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA.把画出的△A′B′C′剪下来,放在△ABC上,它们能完全重合吗?(即全等吗)
【学生活动】拿出直尺和圆规按上面的要求作图,并验证.(如课本图11.2-2所示)
画一个△A′B′C′,使A′B′=AB′,A′C′=AC,B′C′=BC:
1.画线段取B′C′=BC;
2.分别以B′、C′为圆心,线段AB、AC为半径画弧,两弧交于点A′;
3.连接线段A′B′、A′C′.
【教师活动】巡视、指导,引入课题:“上述的生活实例和尺规作图的结果反映了什么规律?”
【学生活动】在思考、实践的基础上可以归纳出下面判定两个三角形全等的定理.
(1)判定方法:三边对应相等的两个三角形全等(简写成“边边边”或“SSS”).
(2)判断两个三角形全等的推理过程,叫做证明三角形全等.
【评析】通过学生全过程的画图、观察、比较、交流等,逐步探索出最后的结论──边边边,在这个过程中,学生不仅得到了两个三角形全等的条件,同时增强了数学体验.
(二)范例点击,应用所学
【例1】如课本图11.2─3所示,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,求证△ABD≌△ACD.(教师板书)
【教师活动】分析例1,分析:要证明△ABD≌△ACD,可看这两个三角形的三条边是否对应相等.

证明:∵D是BC的中点,
∴BD=CD
在△ABD和△ACD中
∴△ABD≌△ACD(SSS).
【评析】符号“∵”表示“因为”,“∴”表示“所以”;从例1可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论(求证)正确的过程.书写中注意对应顶点要写在同一个位置上,哪个三角形先写,哪个三角形的边就先写.
(三)实践应用,合作学习
【问题思考】
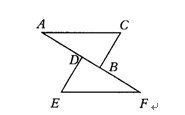
已知AC=FE,BC=DE,点A、D、B、F在直线上,AD=FB(如图所示),要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
【教师活动】提出问题,巡视、引导学生,并请学生说说自己的想法.
【学生活动】先独立思考后,再发言:“还应该有AB=FD,只要AD=FB两边都加上DB即可得到AB=FD.”
【教学形式】先独立思考,再合作交流,师生互动.
(四)随堂练习,巩固深化
课本P8练习.
【探研时空】
如图所示,AB=DF,AC=DE,BE=CF,BC与EF相等吗?你能找到一对全等三角形吗?说明你的理由.(BC=EF,△ABC≌△DFE)

(五)课堂总结,发展潜能
1.全等三角形性质是什么?
2.正确地判断出全等三角形的对应边、对应角,利用全等三角形处理问题的基础,你是怎样掌握判断对应边、对应角的方法?
3.“边边边”判定法告诉我们什么呢?(答:只要一个三角形三边长度确定了,则这个三角形的形状大小就完全确定了,这就是三角形的稳定性)
(六)布置作业,专题突破
1.课本P15习题11.2第1,2题.
2.选用课时作业设计.
(七)板书设计
把黑板平均分成三份,左边部分板书“边边边”判定法,中间部分板书例题,右边部分板书练习.
(八)疑难解析
证明中的每一步推理都要有根据,不能“想当然”,这些根据,可以是已知条件,也可以是定义、公理、已学过的重要结论.



