师:上题在我们共同努力下得以解决,下面看你们自己的表现怎样?
例2 解方程0.5x-0.5= 10 。
学生活动:在练习本上做,一个学生板演.
师生共同订正.
师:这里虽不要求同学们检验,但今后希望同学们养成自我检查的良好习惯.
【教法说明】通过例2的教学训练学生的判断能力及运算能力,树立矛盾转化思想.
(四)变式训练,培养能力
(出示投影2)
1.(口答)解下列方程
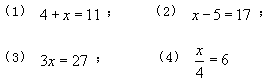

学生活动:1、2题口答,3、4题在练习本上书写,可互相讨论,3、4题师巡回指导。
【教法说明】1题让学生困难同学回答,增强自信心;2题澄清模糊认识,可充分讨论,让学生各抒已见;3题较1题稍复杂,一是让学生体会新解法的优越性,二是培养学生观察分析解决问题的能力;4题其实也是解方程,目的是开阔学生思路,培养学生勇于探索、大胆求异的创新精神。
(五)归纳小结
(由学生归纳)
1.按照新方法解方程,一般采用下面两点:
(1)方程两边都加上(或减去)同一适当的数;
(2)方程两边都乘以(或除以)同一适当的数。
2.为了保证运算准确,养成检验的习惯。
八、随堂练习
1.选择题

九、布置作业
(一)必做题:课本第31页A组1.(2)(4)、 2.(1)(3)(5)
(二)选做题:思考课本B组1、2。
十、板书设计
附:1.5 简易方程
随堂练习答案


探究活动
甲、乙二人从相距30m的两地同向而行,甲每秒走7m,乙每秒走6.5m,如果甲先出发1秒钟后,乙才出发,求甲出发后几秒钟追上乙?
解法(-)设甲出发后x 秒追上乙,则甲走的路程为7x m,乙比甲晚1秒钟出发,乙少走1秒钟,此时,乙走的路程为6.5(x-1) m,甲追上乙表示甲比乙多走30m。根据题意列出方程是:7x= 6.5(x-1)+30
解得 x=47 (秒)
答:甲出发后47秒追上乙.
解法(二)设甲出发后 x 秒追上乙,甲先走1秒钟,甲先走了7*1=7 m,这样甲追上己只需多走 30-7*1=23 (m).这时甲、乙二人都走了(x-1)秒,甲走的路程为 7(x-1) m,乙走的路程为 6.5(x-1) m,乙比甲走的路程少30-7*1=23 (m),根据题意列出方程是:
7(x-1)= 6.5(x-1)+ 7(x-1)
解得x=47 (秒)
答:甲出发后47秒追上乙.
解法(三)设已出发后 x 秒,甲追上乙,因为甲先走1秒,所以甲走了(x+1) ,乙走了x 秒,甲走的路程比已走的路程多30m,依据此等量关系列出方程为: 7(x+1) -6.5x=30
解得 x=46 秒
甲走的时间为x+1=47 (秒)
答:甲出发后47秒追上乙.
